sommaire

SDR Radio par Logiciel

 SDR :  RADIO par LOGICIEL ( mes premiers pas ! )

La technique évolue depuis quelques années, avec l'apparition de l'ordinateur ou de calculateurs dans les appareils à la place de composants électroniques. L'avantage de cette solution est une grande souplesse, puisqu'il y a une facilité de configuration : "la radio reconfigurable". En contre partie, la complexité augmente et on est loin du concept de "la radio mais c'est très simple" !  Il faut reprendre les livres de maths, et apprendre la programmation. Rien que ça ! 

Comme tous les radioamateurs un peu curieux de cette évolution, et cherchant à réaliser des projets et des expérimentations, je propose de commencer une série de pages sur ce sujet, ne sachant pas trop dans quelle direction aller ? Je me jette à l'eau ! 

La première chose à faire est de récupérer des informations sur le SDR, une quantité d'articles est disponible sur le site de l ' ARRL et des articles en français commencent à paraître dans notre revue du REF. Une collection de fichiers au format PDF est donc constituée facilement, reste à traduire les textes et à chercher comment faire pour avancer dans cette technique, par quel bout commencer ? 

Mon objectif est donc de découvrir au fur et à mesure, de quoi il s'agit et d'essayer de rendre les choses simples et claires, un peu comme jadis dans le livre de E.Aisberg : "la radio ?.. mais c'est très simple". La différence est qu'il n'y aura pas de dialogue entre celui qui sait tout ( Curiosus ) et celui qui ignore tout ( Ignotus ) puisque je suis plutôt comme le second personnage, mais comme disait Monsieur  Aisberg dans son livre, il ignore bien des choses mais il n'est assurément pas bête !

Pour avancer, rapidement, je compte sur les radioamateurs qui comme moi, vont se lancer dans cette technique, surtout ceux des clubs, et nous pourrons envisager ensemble quelques réalisations pratiques pour vérifier nos belles théories. 

Le début :  le vecteur tournant ! 

Nous savons tous qu'un signal sinusoïdal, par exemple la tension alternative du réseau électrique est une tension qui varie suivant une équation de type sinusoïde.

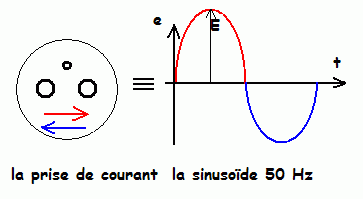
Pour la première demi période, la tension est positive, pour la demi période suivante, le tension est négative, d'où le nom de tension alternative par rapport au zéro de tension. La tension alternative varie dans le temps en fonction de la période et donc de la fréquence. Pour l'exemple du réseau électrique, la fréquence est de 50 hertz et la période est de  1 / 50  =  0,02 s. 

Mais pourquoi, parler de sinusoïde ? Il faudrait pour expliquer ceci montrer comment est produit le courant électrique, à l'aide d'une machine qui se nomme justement un alternateur. L'alternateur le plus simple à réaliser se fait avec un aimant qui tourne au milieu d'une bobine de fil électrique.

Une autre solution consiste à faire tourner une bobine de fil ( ou cadre ) au milieu d'un aimant en U, c'est alors une génératrice avec des bagues ou un collecteur et des balais qui va redresser le courant pour produire du courant continu ( penser à une tension non pas alternative mais toujours du même côté : d' où le terme de continu ). 

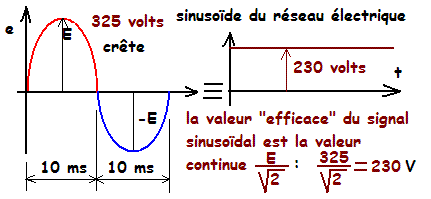
Pour représenter la tension alternative, il y a deux représentations : 

--- la représentation cartésienne  :   la tension en fonction du temps.       y  =   fonction de  t   

--- la représentation de Fresnel  :   le vecteur tournant à la vitesse  angulaire  w   c'est  un angle parcouru en fonction du temps  w   =    Q  /   t  

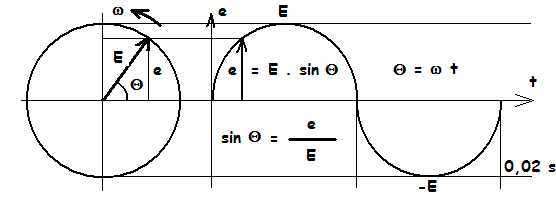
l'angle exprimé en radians et le temps en seconde, la vitesse est exprimée en radians par seconde. Rotation anti horaire. 

Revenons à l'alternateur et cherchons l'équation de la tension alternative : 

Le champ magnétique de l'aimant est  B, la surface d'une spire de bobine est S, le nombre de spires est N. A l'instant de départ, la bobine est horizontale et le flux est maximum dans la bobine :   

F total   =   B . S . N              (  le flux magnétique c'est l'induction magnétique multiplié par la surface traversée ). 

Quand la bobine a tourné de l'angle   a   =   w   .    t    le flux  embrassé par la bobine est plus faible  :   multiplié par  cos   a

F   =    F  total .  cos    w .   t       =    B  .   S   .   N  .  cos    w  .   t 

La force électromotrice induite ( ou tension induite dans la bobine )  est donnée par la loi de Lenz   ( pour une spire )   :    la  FEM *   est la dérivée du flux. C'est la variation du flux qui produit la tension induite. Au plus la variation est rapide, au plus la tension est forte. On écrit  :   

e   =    -    d  F   /    d  t       =     -  (  F  total ) .  (  -  w  .   sin  w   .   t   )    =    B .  S  .  N  .   w    .   sin    w   .   t    =    E  .    sin  w   .  t  

La tension alternative a pour équation  :    e   =   E  .   sin  w   .  t     c'est bien une sinusoïde, avec  E  la valeur de crête.  

(  La dérivée  de   K .  cos  a .  x      est    égale   à    -   K   .  a   .  sin  a .  x   )

Si on prend  la projection  du vecteur tournant  E  à la vitesse  angulaire   w   (  celle de la bobine tournante )  sur l' axe vertical,  on retrouve  l'équation de la sinusoïde, c'est à dire la valeur de la tension e  en fonction du temps. 

Pour un tour du vecteur  (   pour un angle de  360° ou  2 p ,  on peut dire aussi  6, 28 radians )  à  la vitesse  angulaire   w  =   a   /   t  ,  on peut écrire  :

W  =      2   .   p    /    T                        W    =      2  .   p   .   F                  par exemple :   une bobine tourne à  3000 tours par minutes, la fréquence de la tension est

trouvée avec cette relation.  On sait  que  pour passer des tours par minute aux radians par seconde   W   =    (  2  .   p   .  n  )  /  60    

W   =    (  2  .   p   .  3000   )  /  60    =   314,16  radians /sec   

F  =   W   /    2  .   p   =    314, 16  /     2  .   p   =    50   hertz.    Conclusion :  un alternateur qui tourne à  3000 tr / min donne une tension à  fréquence de 50 Hz. 

Remarques importantes : 

--- La pulsation est   w ,  c'est la vitesse angulaire du vecteur tournant en rad/s   :     w    =      2  .   p   .   F      avec  F  la  fréquence en hertz. 

--- Origine des temps :  si à l'origine des temps (  t = 0 )  le vecteur est dans une position quelconque  dans sa rotation anti horaire (  angle  Q  ), la phase de la fonction est alors égale à   :   

l'angle parcouru  a  depuis l'origine des temps  plus l'angle  à l'origine des temps   Q    :    la phase est  (  a   +  Q   )    ou   (   w  .  t   +   Q   )

--- La valeur de la fonction est alors dans un cas général  :    e  =   E  .   sin   (   w  .  t   +   Q   ) cette forme  est valable pour n'importe quelle fréquence.

--- On pourrait écrire aussi  :      e  =   E  .   cos   (   w  .  t   +   Q   )    et  parler de fonction cosinusoïdale. 

On peut dire que  cos  x   =   sin  (  x  +   p  / 2 )       Voir formulaire de trigo !

d'où   e  =   E  .    sin  (  w  .  t   +   Q    +   p  / 2   )      c'est toujours une fonction sinusoïdale !  La phase à l'origine est     (   Q    +   p  / 2   ).

On parlera toujours de fonction sinusoïdale. 

à suivre,  le modulateur à quadrature. On utilisera la forme :  e  =   E  .   cos   (   w  .  t   +   Q   )

*  FEM  voulait dire :  la force qui met l'électricité en mouvement, on a conservé cette expression pour le cas d'une tension.

©2002 concept par SIECLE21 (F6AGV) toute reproduction autorisée si mention du site. Mise à jour le : 04/08/2009